GPU-Accelerated Subgraph Enumeration on Partitioned Graphs

A paper at the SIGMOD 2020 conference.

其他是建立在 GPU 能放下数据图，或者数据图在主存中，通过采取合适的数据来传入 GPU 进行处理。

这个方法是直接分区，块中的内容不需要再调用主存。但是分区间仍然存在传输问题。

CPU-based Subgraph Enumerations

  • Single-machine subgraph enumeration

    • Built upon the Ullman‘s work

      • A selective search sequence

      • Various pruning techniques

        • Non-indexed approaches

          To apply a series of feasibility rules. For example, we can invalidate unpromising partial instances beforehand.

        • Indexed approaches

        To build the indexes that can prune partial instances as early as possible.

        But it seems that the indexed approaches may not help.

  • Distributed subgraph enumeration

    • Rely on distributed frameworks

GPU-based Subgraph Enumeration

Two major previous studies

  • NEMO
  • GPSM

  • COMPUTE：计算出来所有可能性。

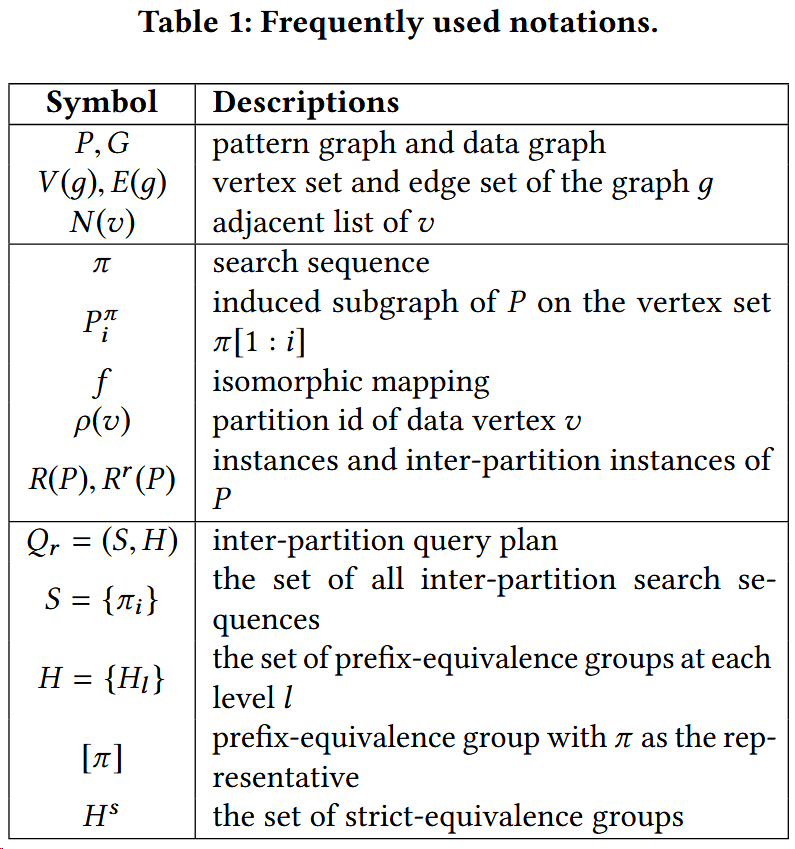
    • $\pi(l)$: the $l^{th}$ vertex of $\pi$

    • $P^{\pi}_{i}$: subgraph of P on the vertex set π [1 : i]

    • $R(P)$: instances of P

    • $\pi ^{-1}(u)$: the ordinal position of $u$ in $\pi$

    • $N_{+}(u)$: In search sequence, the adjacent list of u and the vertex that before u in $\pi$

    • $C(u|f)$: for f and u, the set of possible candidate data vertices

  • MATERILALIZE：循环，将新的实例都输出在记录在新的$P^{\pi}_{l}$中，有点像 DP 的思想。

$\pi={u_1,u_2,u_3}$

$R(P^{\pi}_{1})={(u_1,v_1)},{(u_1,v_2)},{(u_1,v_3)},{(u_1,v_4)}$

$C2 = COMPUTE(u_2,\pi,R(P^{\pi}{1}))$

$N_+(u_2)={u_1}$

  • $f={{(u_1,v_1)}}$
    • $C(u_2|{(u_1,v_1)})={v_2,v_3,v_4}-{v_1}={v_2,v_3,v_4}$
  • $f={{(u_1,v_2)}}$
    • $C(u|f)={v_1,v_3,v_4}-{v_2}={v_1,v_3,v_4}$
  • $f={{(u_1,v_3)}}$
    • $C(u|f)={v_1,v_2,v_4}-{v_3}={v_1,v_2,v_4}$
  • $f={{(u_1,v_4)}}$
    • $C(u|f)={v_1,v_2,v_3}-{v_4}={v_1,v_2,v_3}$

$R(P^{\pi}_{2})=MATERIALIZE(u_2,\pi,R(P_1^\pi),C)$

$R(P_2^\pi) = $

${(u_1,v_1),(u_2,v_2)},{(u_1,v_1),(u_2,v_3)},{(u_1,v_1),(u_2,v_4)},$

${(u_1,v_2),(u_2,v_1)},{(u_1,v_2),(u_2,v_3)},{(u_1,v_2),(u_2,v_4)},$

${(u_1,v_3),(u_2,v_1)},{(u_1,v_3),(u_2,v_2)},{(u_1,v_3),(u_2,v_4)},$

${(u_1,v_4),(u_2,v_1)},{(u_1,v_4),(u_2,v_2)},{(u_1,v_4),(u_2,v_3)}$

$C3 = COMPUTE(u_3,\pi,R(P^{\pi}{2}))$

$N_+(u_3)={u_1,u_2}$

  • $f={(u_1,v_1),(u_2,v_2)}$
    • $C(u_3|{(u_1,v_1)(u_2,v_2)})={v_4}-{v_1,v_2}={v_4}$
  • ....

$R(P^{\pi}_{3})=MATERIALIZE(u_3,\pi,R(P_2^\pi),C)$

$R(P_3^\pi) = $

${(u_1,v_1),(u_2,v_2),(u_3,v_4)},...$

PARTITION BASED ENUMERATION

We use the standard graph partition approach, i.e., METIS

results matching ""

    No results matching ""